抱着纯属玩票的心态看完了 Andrew Ng 的机器学习入门课,又恰逢期末课设,就想着利用神经网络做一个简单数学表达式的识别和求值工具,主要的模型训练和识别部分都是由 Matlab 完成。
神经网络模型
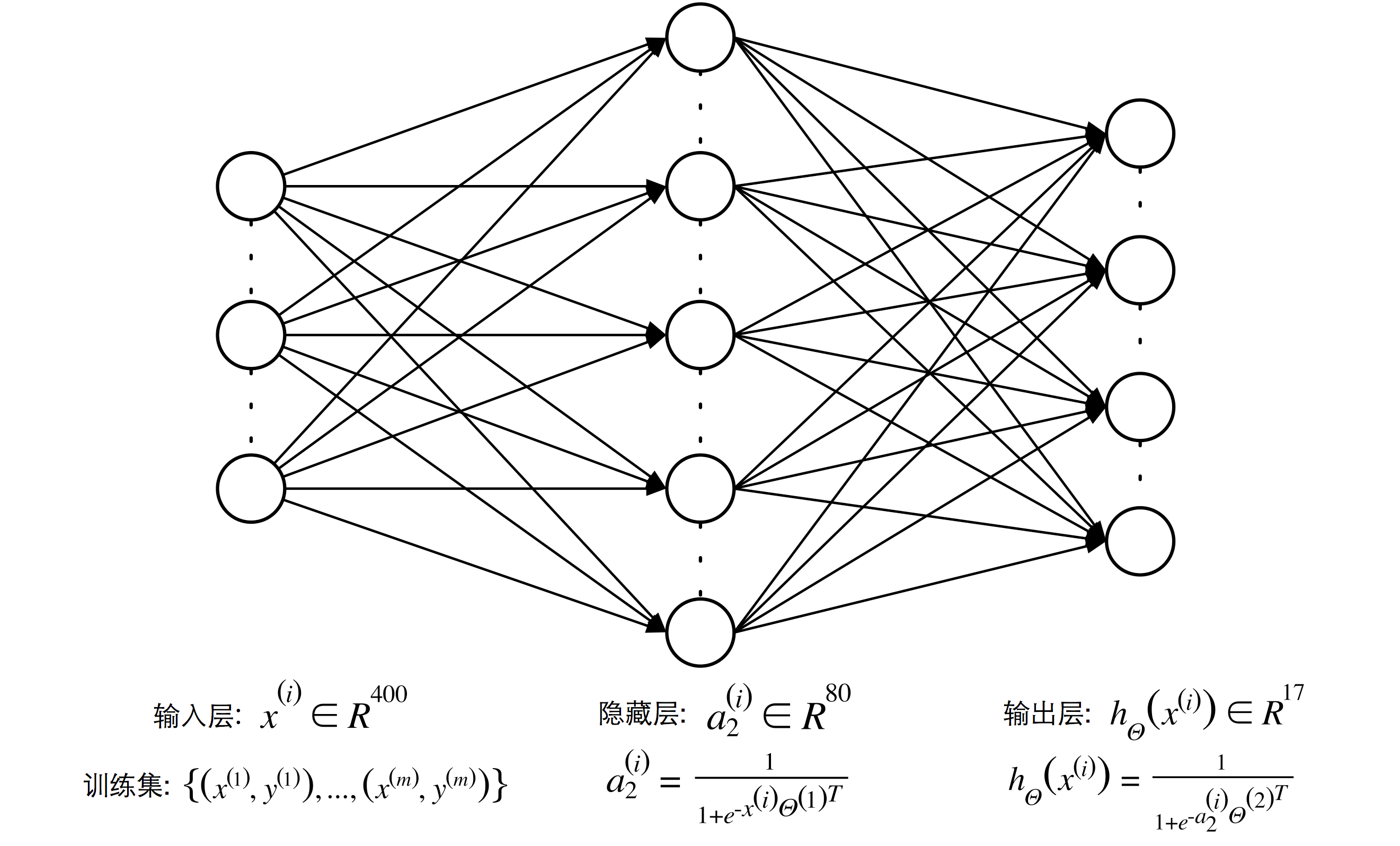
考虑到计算速度,我只建立了一个简单的三层 BP 神经网络模型作为分类器来识别单个字符,模型简化图如上。输入层是由 20x20 的图像得到的 1x400 的特征向量,隐藏层共 80 个隐藏单元,激活函数采用 sigmoid function,输出层是一个 1x17 的向量,可以用来描述 17 种识别结果:数字 0-9 和 +, -, ⨯, ÷, ^, (, )。
数据集和预处理
-
同样也是出于计算速度的考虑,以及需要识别的除了数字还有符号,我没有使用只含数字且较大的 MNIST 数据集,而是找室友一起手写了大概 1000 个数字和符号作为训练数据。
-
不管是用作训练数据的图像还是最终需要识别的图像都需要做预处理,把图片上表达式的每个字符分离成单独的图像再依次送至分类器识别,预处理也是用 Matlab 完成,具体过程如下:
- 图像转为灰度图像后反色处理,并进行中值滤波以平滑图像,然后进行整体边界限定,截取表达式区域图像。
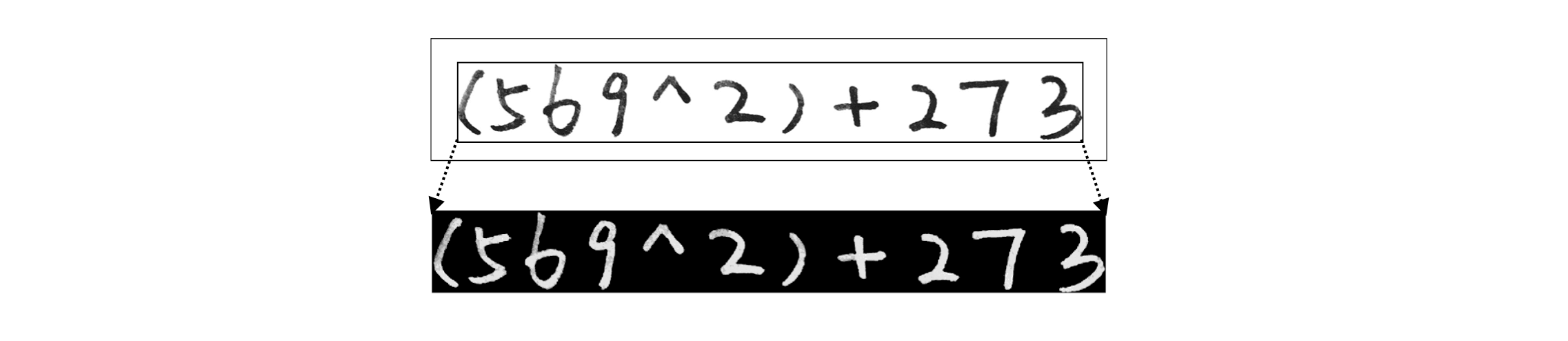
- 横向提取并拼接有效行,纵向提取并分割有效字符。提取每个分割区域为独⽴图像,进行边界限定,计算灰度阈值并转为⼆值图像,最后大小归一化图像:填充至正方形并统一为 20x20 的图像。

预处理部分还需要注意的主要问题是过滤噪音,除了平滑图像和边界限定以外,还要剔除掉高度过小的行、宽度过小的列以及面积过小的区域。完整代码见这里:https://github.com/Wildog/handwritten-expr-evaluator/blob/master/getPicChar.m
- 图像转为灰度图像后反色处理,并进行中值滤波以平滑图像,然后进行整体边界限定,截取表达式区域图像。
训练模型
- 首先是随机初始化权重,避免每层的每个单元学习到同样的参数。本质就是给每个权重矩阵里面的每个权重设置一个介于 [-𝜺, 𝜺] 的值,这个 𝜺 一般取
sqrt(6) / sqrt(input_layer_size + output_layer_size),完整函数如下:
function W = randInitializeWeights(L_in, L_out)
% 由于 bias unit 的存在,权重矩阵的实际大小是 L_out * (1 + L_in)
W = zeros(L_out, 1 + L_in);
epsilon_init = sqrt(6) / sqrt(L_in + L_out);
W = rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init;- 训练模型的本质就是不断地迭代学习利用梯度下降法最小化代价函数。在每轮迭代中,先使用前向传播算法计算各层输出值,再使用后向传播算法计算各层残差以计算各个权重矩阵的梯度,并计算代价函数,我写的一轮迭代如下:
function [J grad] = nnCostFunction(nn_params, ...
input_layer_size, ...
hidden_layer_size, ...
num_labels, ...
X, y, lambda)
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
num_labels, (hidden_layer_size + 1));
m = size(X, 1);
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));
for i = 1:m
%Forward Propagation 算法计算各层输出值
hidden_layer = zeros(hidden_layer_size,1);
input_layer = [1; X(i,:)'];
hidden_layer = [1; sigmoid(Theta1 * input_layer)];
output_layer = zeros(num_labels,1);
output_layer = sigmoid(Theta2 * hidden_layer);
y_recode = zeros(num_labels,1);
y_recode(y(i)) = 1;
%Backpropagation 算法计算各层残差以计算 Theta1 和 Theta2 的梯度
delta3 = output_layer - y_recode;
delta2 = Theta2' * delta3 .* (hidden_layer .* (1 - hidden_layer));
delta2 = delta2(2:end); %!!!丢弃 bias unit
%累加梯度
Theta1_grad = Theta1_grad + delta2 * input_layer';
Theta2_grad = Theta2_grad + delta3 * hidden_layer';
%累加 LR cost
J = J + y_recode' * log(output_layer) + (1 - y_recode') * log(1 - output_layer);
end
%计算 NN cost
J = -(1/m) * J + lambda/(2*m) * (sum(sum(Theta1(:, 2:end).^2)) + sum(sum(Theta2(:, 2:end).^2)));
Theta1_temp = Theta1_grad;
Theta1_grad = (1/m) * Theta1_grad + (lambda/m) * Theta1;
tmp1 = ((1/m) * Theta1_temp);
Theta1_grad(:,1) = tmp1(:,1);
Theta2_temp = Theta2_grad;
Theta2_grad = (1/m) * Theta2_grad + (lambda/m) * Theta2;
tmp2 = ((1/m) * Theta2_temp);
Theta2_grad(:,1) = tmp2(:,1);
grad = [Theta1_grad(:) ; Theta2_grad(:)];这个函数会返回一轮迭代后的代价函数值和各个权重矩阵的梯度,给这个函数创建一个句柄,设置一下学习率和最大迭代次数,和随机初始化后的各权重矩阵一起传给 fmincg 函数计算,然后静静地等着代价函数收敛就行了,不断的测试准确率再反复更改参数重新训练,最后得到满意的各权重矩阵。
大功告成
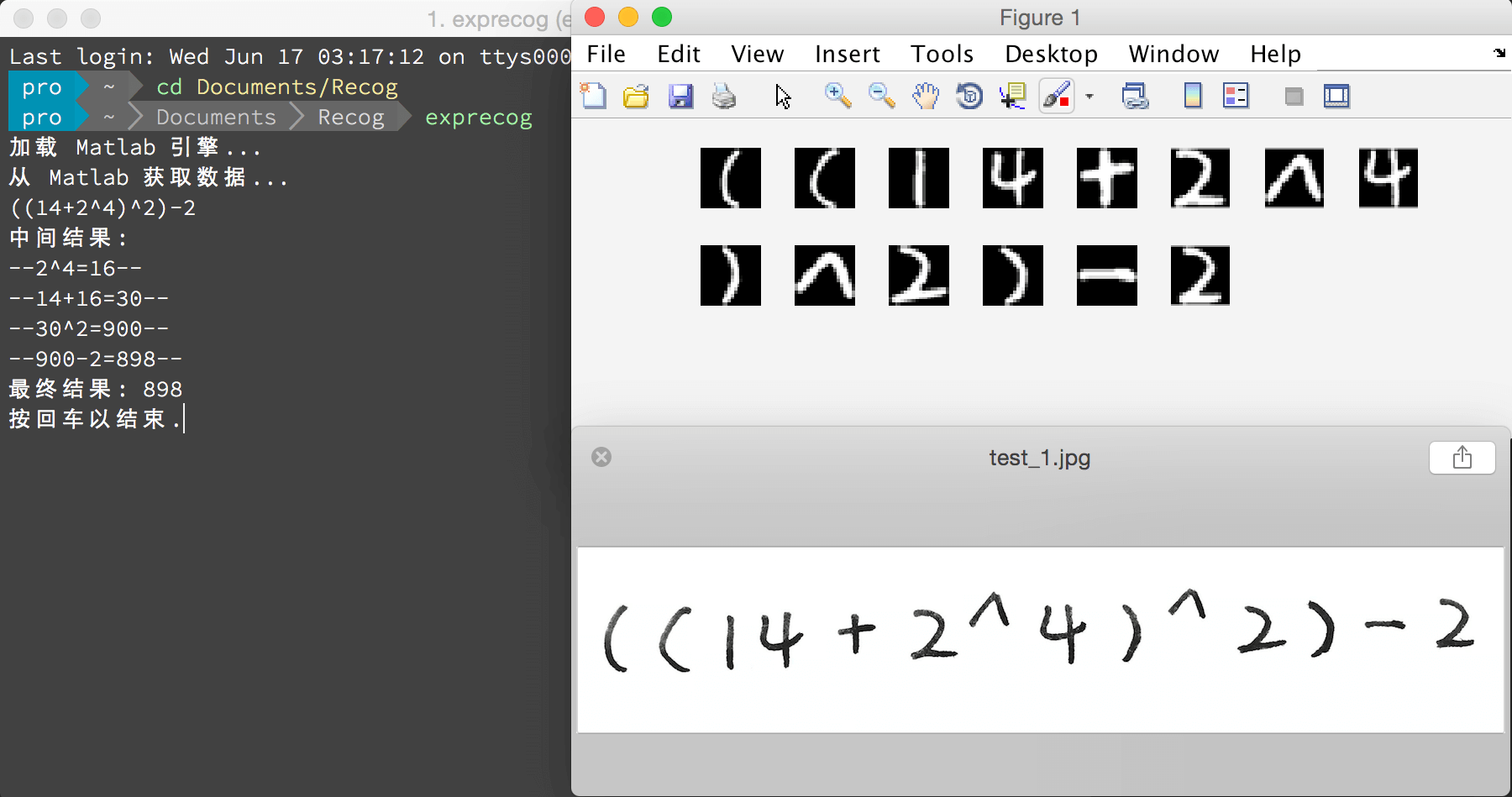
得到最终的权重矩阵后,针对预处理后的每个字符图像的像素矩阵计算其输出层就可以识别出对应的字符了,依次识别每个字符最终得到整个表达式,剩下的计算表达式的方法太多了不再多提,晒下结果图: